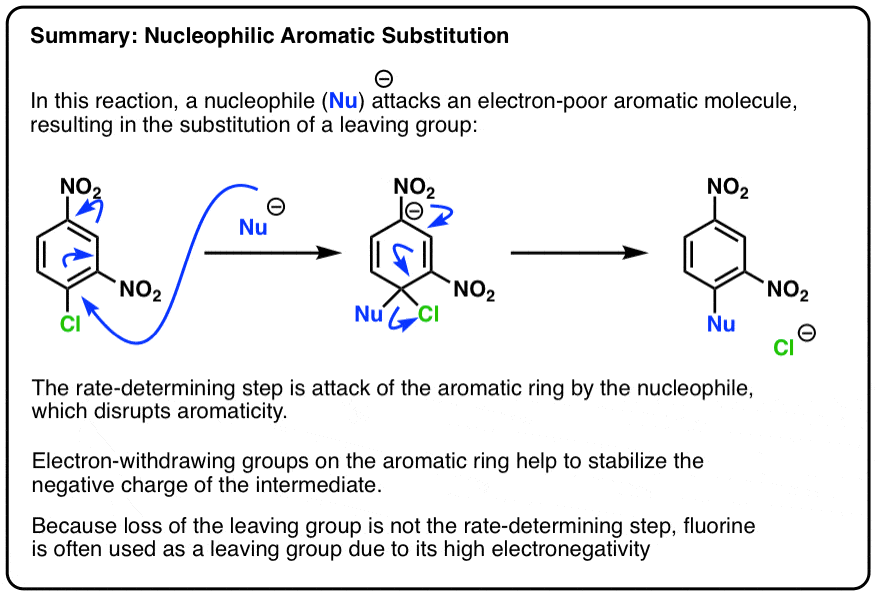
Nucleophilic Aromatic Substitution (NAS) - with reaction mechanism

Not The Aromatic Substitution Reaction You Were Expecting

Let’s review electrophilic aromatic substitution (EAS). What have we learned?

• The aromatic ring behave as a nucleophile, and attacks an added electrophile 
• An electron-deficient carbocation intermediate is formed (that is, the rate-determining step) which is then deprotonated to restore aromaticity
• electron-donating groups on the aromatic ring (such as OH, OCH₃, and alkyl) make the reaction faster, since they help to stabilize the electron-poor carbocation intermediate
• Lewis acids can make electrophiles even more electron-poor (reactive), increasing the reaction rate. For example  FeBr₃ / Br₂allows bromination to occur at a useful rate on benzene, whereas Br₂ by itself is slow).

Everything we have learned so far about substitution on aromatic rings would make us understand that it proceeds much faster with methoxybenzene than with nitrobenzene, and much faster with an electrophile like Cl₂ than with, say, an electron-rich nucleophile like NaOCH₃.

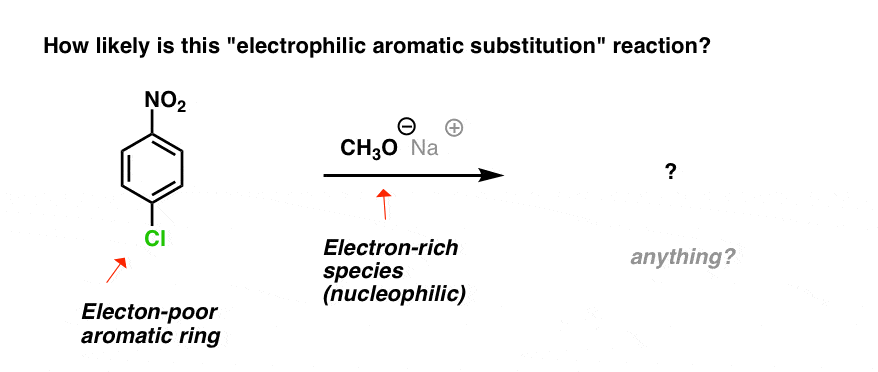
Which brings us to the reaction below. The aromatic ring  is electron-poor and we’re adding an electron-rich nucleophile.

What could happen here? Nothing, right?

“Nothing” is a good guess! Certainly, thinking of this as an electrophilic aromatic substitution, you’d be right in thinking that the answer to “what happens here?” is “jack squat”.

Nucleophilic Aromatic Substitution

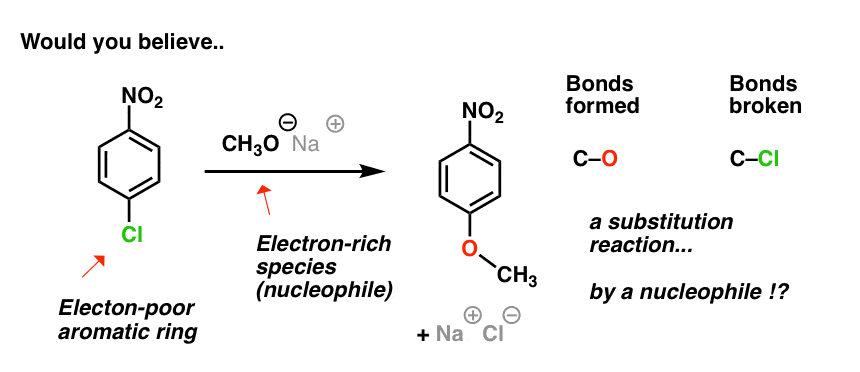
In fact, a substitution reaction does occur! (But, as you may suspect, this isn’t an electrophilic aromatic substitution reaction.)

In this substitution reaction the C-Cl bond breaks, and a C-O bond forms on the same carbon.

So while it is a substitution reaction, it has a few important differences:

• The species that attacks the ring is a nucleophile, not an electrophile
• The aromatic ring is electron-poor (electrophilic), not electron rich (nucleophilic)
• The “leaving group” is chlorine, not H+
• The position where the nucleophile attacks is determined by where the leaving group is, not by electronic and steric factors (i.e. no mix of ortho– and para- products as with electrophilic aromatic substitution).

In short, the roles of the aromatic ring and attacking species are reversed!

The attacking species (CH₃O^–) is the nucleophile, and the ring is the electrophile.

Since the nucleophile is the attacking species, this type of reaction has come to be known as nucleophilic aromatic substitution. 

1. The Effect Of Substituents On The Ring

In nucleophilic aromatic substitution (NAS), all the trends you learned in electrophilic aromatic substitution operate, but in reverse.

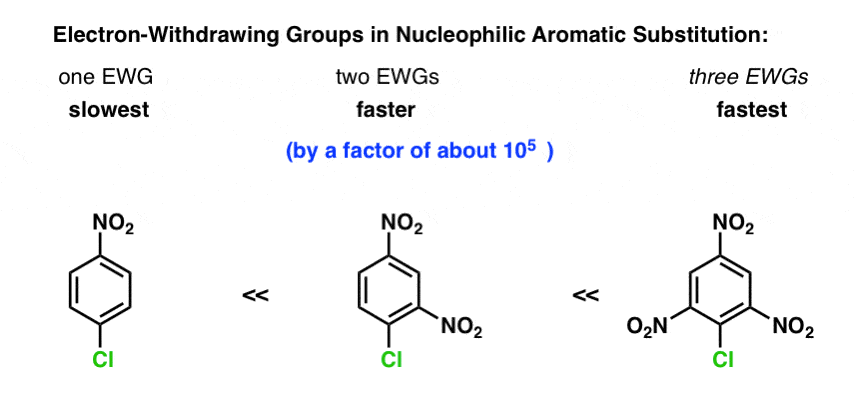
The first trend to understand is that electron withdrawing groups (EWG’s) dramatically increase the rate of reaction, not decrease it.

From this, it follows that the more EWG’s there are, the faster the reaction.

For example, the rate of NAS for 2,4-dinitrophenyl chloride is about 10⁵ times faster than for p-nitrophenyl chloride. [note]

(I don’t have a rate constant for 2,4,6-trinitrophenyl chloride readily available, but it is orders of magnitude faster still).

2. The Effect Of The Leaving Group

One of the most eye-opening aspects of nucleophilic aromatic substitution is noting that fluorine is often used as a leaving group. This is seen in Sanger's reagent for sequencing peptides, to take one example (more on that below).

After all, given the stern tones we instructors use in Org 1 on this subject, the words  “FLUORINE IS NEVER A LEAVING GROUP IN S_N2 AND S_N1 REACTIONS” may as well have been carved on one of the stone tablets handed down to Moses on Mt. Sinai.

Here’s a thought: if even a “bad” leaving group like fluorine works in nucleophilic aromatic substitution, then surely a “better” leaving group like bromine or iodine would work even better. Right?

For one reaction studied, F as the leaving group  was observed to be 3300 times faster than iodine !

And between chlorine, bromine, and iodine, the difference was only by a factor of about 3.

So what could be different about nucleophilic aromatic substitution that makes the rate of reaction much less sensitive to the identity of the leaving group than the S_N1 and S_N2 reactions?

Well, for one thing, this would suggest that, unlike the S_N1 and S_N2 reactions, C-F bond cleavage does not occur in the rate-determining step. This information is helpful in coming up with a mechanism for the reaction.

3. The Effect Of Substitution Pattern

Unlike in electrophilic aromatic substitution, there are no “ortho-,para-” or “meta-” directors. The position of substitution is controlled by the placement of the leaving group.

However that isn’t to say that the rate of the reaction isn’t affected by the relative position of the leaving group and the electron-withdrawing group.

For example, nucleophilic aromatic substitution of p-nitrophenyl fluoride is orders of magnitude faster than m-nitrophenyl fluoride, even though the NO2 is closer to the leaving group and should presumably exert more of an inductive effect.

The ortho isomer is also faster than the metaby a large margin.

What’s going on? 

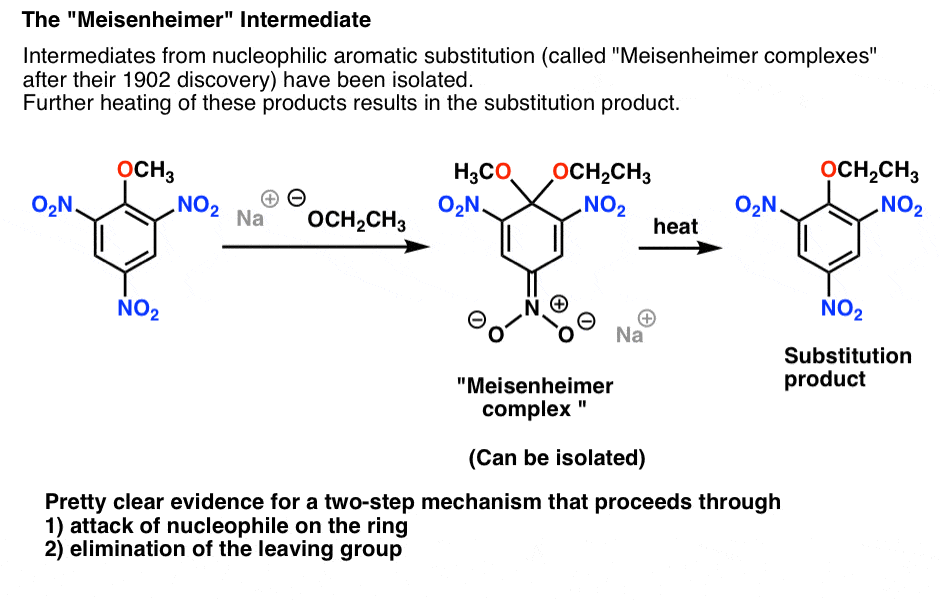
4. The “Meisenheimer” Intermediate Provides A Clue To The Mechanism

In the course of adding nucleophiles to various electron-poor aromatic molecules with a leaving group, intermediates have been isolated. One of the first was isolated in 1902 by Jacob Meisenheimer, and the general name “Meisenheime's complex” is given to these intermediates.

The intermediate is the (non-aromatic) addition product between the aromatic ring and the nucleophile. In the case below, the negative charge is delocalized to an oxygen on one of the nitro groups:

Meisenheimer intermediates can be isolated and characterized. However, if heated, the compound goes on to form the final nucleophilic aromatic substitution product.

This is very suggestive, to say the least.

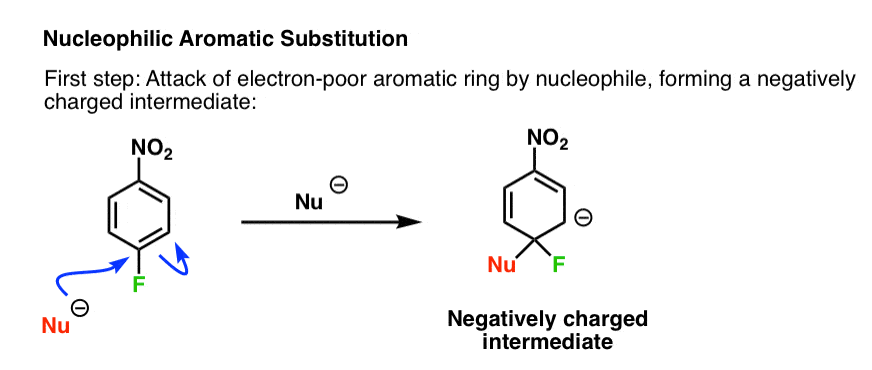
5. The Mechanism

Taking all of these observations into account we can now propose a mechanism for this reaction.

The first step is attack of the nucleophile on the electron-poor ring to generate a negatively charged intermediate (e.g. the “Meisenheimer” intermediate, above)

Since this disrupts the aromaticity of the ring, it’s also the rate-limiting step:

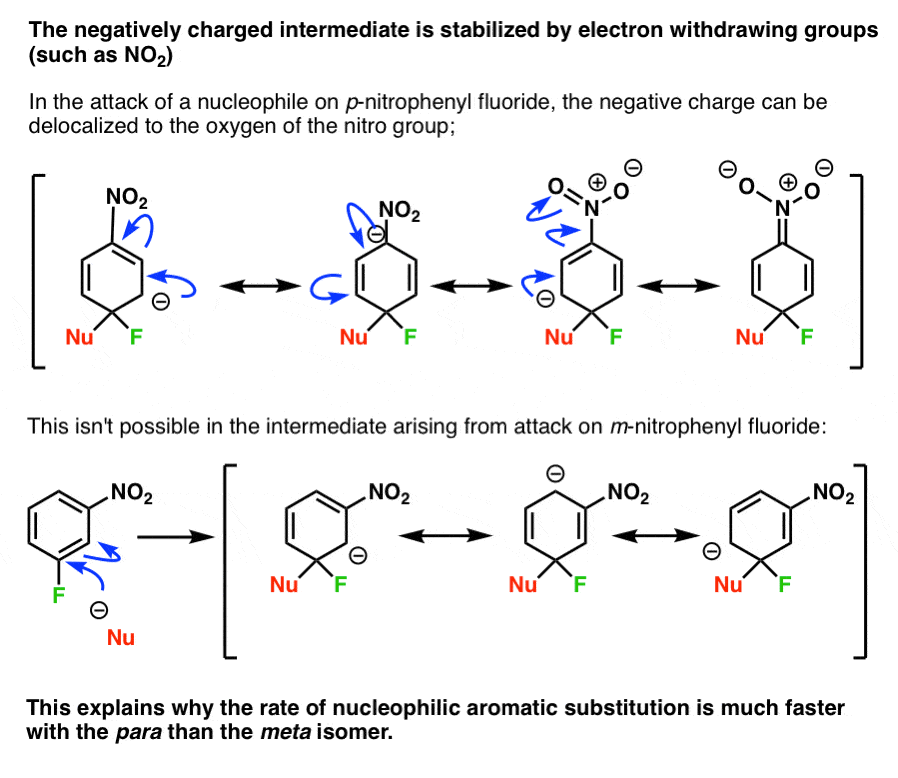
In electrophilic aromatic substitution (EAS) we saw that electron-rich substituents stabilized the electron-poor intermediate.

But in nucleophilic aromatic substitution (NAS) the tables are turned!  Instead, the intermediate is electron-rich, and is stabilized by electron-withdrawing substituents, such as NO₂.

The second step in nucleophilic aromatic substitution is expulsion of the leaving group:

This two-step mechanism where addition is the rate-determining step helps to explain our earlier puzzle of why the reaction with para-nitro is faster than the meta- isomer.

Note how the anion in the para- intermediate can be delocalized to the oxygen on the nitro group, putting a negative charge on (more electronegative) oxygen.

In the meta- intermediate, the negative charge cannot be delocalized to the nitro group, and is stuck on (less electronegative) carbon.

(This also explains why addition is fast for the ortho– isomer).

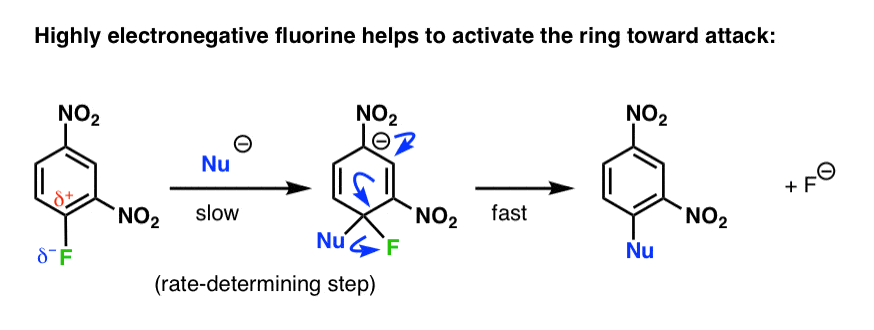
It also helps to explain why fluorine substituents increase the rate of nucleophilic aromatic substitution: the rate determining step is attack on the aromatic ring, not breaking the very strong C-F bond. The highly electronegative fluorine pulls electron density out of the ring, activating it towards attack.

So even though breaking a C-F bond is generally not energetically favorable, this is compensated by the fact that it restores aromaticity.

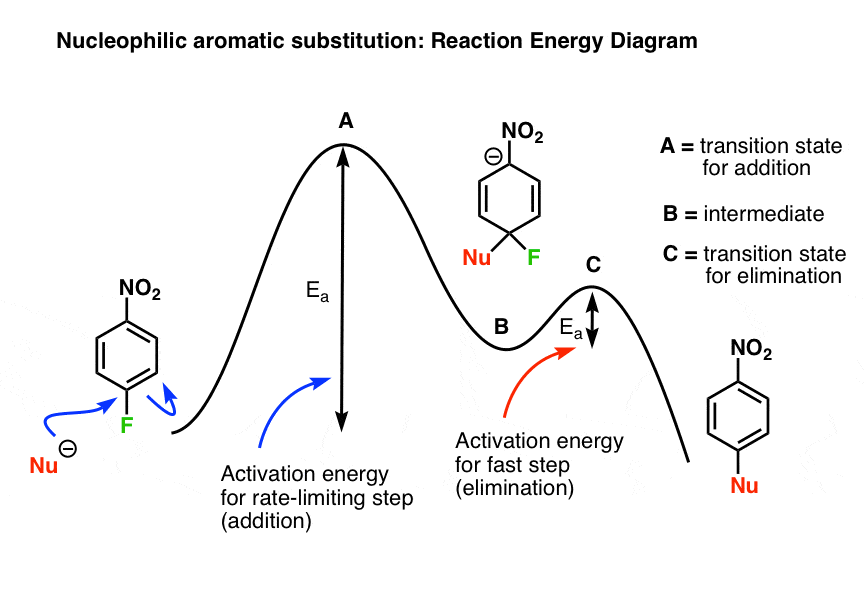
6. The Reaction Energy Diagram

Putting it all together, we can sketch out a reaction-energy diagram for this mechanism that would look something like this:

(remember: transitition states are “peaks”, and intermediates are “valleys”. Intermediates can (at least theoretically) be isolated; transition states have partial bonds, only last a femtosecond, and can’t be isolated).

The nucleophile adds to the aromatic ring through transition state A (the rate limiting step) to give the negatively charged intermediate B, with a further input of energy (Ea) ascends to transition state C (loss of the leaving group, the fast step) and from there, the final product.